Ejercicios paginas 157 y 158
Ejercicios pagina 157 y 158
5.29 Si se reparten 7 cartas de una baraja ordinaria de 52 cartas, ¿cuál es la probabilidad de que
a) exactamente 2 de ellas sean mayores a 10?
b) al menos 1 de ellas sea una reina?
5.30 Para evitar la detección en la aduana, un viajero coloca seis comprimidos con narcóticos en una botella que contiene 9 píldoras de vitamina que son similares en apariencia. Si el oficial de la aduana selecciona 3 de las tabletas al azar para su análisis, ¿cuál es la probabilidad de que el viajero sea arrestado por posesión ilegal de narcóticos?
5.31 El dueño de una casa planta 6 bulbos seleccionados al azar de una caja que contiene 5 bulbos de tulipán y cuatro de narciso. ¿Cuál es la probabilidad de que plante 2 bulbos de narciso y 4 de tulipán?
5.32 De un lote de 10 proyectiles, se seleccionan 4 al azar y se lanzan. Si el lote contiene tres proyectiles defectuosos que no explotarán, ¿cuál es la probabilidad de que
a) los 4 exploten?
b) a lo más 2 fallen?
5.33 Se selecciona al azar un comité de 3 personas a partir de 4 doctores y 2 enfermeras. Escriba una fórmula para la distribución de probabilidad de la variable aleatoria X que representa el número de doctores en el
comité. Encuentre P(2 ≤ X ≤ 3).
5.34 ¿Cuál es la probabilidad de que una mesera se rehusé a servir bebidas alcohólicas a sólo dos menores si ella verifica al azar las identificaciones de 5 estudiantes de entre 9 estudiantes, de los cuales 4 no tienen la edad legal para beber?
5.35 Una compañía está interesada en evaluar su procedimiento de inspección actual en embarques de 50 artículos idénticos. El procedimiento consiste en tomar una muestra de 5 y pasar el embarque si no se encuentran más de 2 defectuosos. ¿Qué proporción de embarques con 20% defectuosos se aceptará?
5.36 Una compañía fabricante utiliza un esquema de aceptación de producción de artículos antes de que se embarquen. El plan tiene dos etapas. Se preparan cajas de 25 artículos para su embarque y se prueba una muestra de 3 en busca de defectuosos. Si se encuentra
alguno defectuoso, toda la caja se regresa para verificar el 100%. Si no se encuentran defectuosos, la caja se embarca.
a) ¿Cuál es la probabilidad de que se embarque una caja que contiene 3 defectuosos?
b) ¿Cuál es la probabilidad de que una caja que contenga sólo 1 artículo defectuoso se regrese para su revisión?
5.37 Suponga que la compañía fabricante del ejercicio 5.36 decide cambiar su esquema de aceptación. Con el nuevo esquema un inspector toma un artículo al azar, lo inspecciona y después lo reemplaza en la caja; un segundo inspector hace lo mismo. Finalmente, un tercer inspector lleva a cabo el mismo procedimiento. La caja no se embarca si cualquiera de los tres encuentra uno defectuoso. Responda el ejercicio 5.36 con este nuevo plan.
5.38 En el ejercicio 5.32, ¿cuántos proyectiles defectuosos se pueden incluir entre los 4 que se seleccionan?
Utilice el teorema de Chebyshev para describir la variabilidad del número de proyectiles defectuosos que se incluyen cuando se seleccionan 4 de varios lotes, cada uno de tamaño 10 con 3 proyectiles defectuosos.
5.39 Si a una persona se le reparten varias veces 13 cartas de una baraja ordinaria de 52 cartas, ¿cuántas cartas de corazones por mano puede esperar? ¿Entre cuáles dos valores esperaría que cayera el número de corazones al menos 75% de las veces?
5.40 Se estima que 4000 de los 10,000 residentes con derecho al voto de una ciudad están en contra de un nuevo impuesto sobre ventas. Si se seleccionan al azar 15 votantes y se les pide su opinión, ¿cuál es la probabilidad de que a lo más 7 estén a favor del nuevo impuesto?
5.41 Una ciudad vecina considera una petición de anexión de 1200 residencias contra una subdivisión del condado. Si los ocupantes de la mitad de las residencias objetan la anexión, ¿cuál es la probabilidad de que en una muestra aleatoria de 10 al menos 3 estén a favor de la petición de anexión?
5.42 Entre 150 empleados de IRS en una ciudad grande, sólo 30 son mujeres. Si se eligen al azar 10 de los aspirantes para que proporcionen asistencia libre de impuestos a los residentes de esta ciudad, utilice la aproximación binomial a la hipergeométrica para encontrar la probabilidad de que al menos 3 mujeres se seleccionen.
5.43 Una encuesta a nivel nacional de la Universidad de Michigan a 17,000 estudiantes universitarios de último año revela que casi 70% desaprueba el consumo de mariguana. Si se seleccionan al azar 18 de tales estudiantes y se les pide su opinión, ¿cuál es la probabilidad de que más de 9 pero menos de 14 desaprueben el consumo de mariguana?
5.44 Encuentre la probabilidad de que cuando se le reparta una mano de bridge de 13 cartas tenga 5 de espadas, 2 de corazones, 3 de diamantes y 3 de tréboles.
5.45 Un club de estudiantes extranjeros tiene como miembros a 2 canadienses, 3 japoneses, 5 italianos y 2 alemanes. Si se selecciona al azar un co mité de 4, encuentre la probabilidad de que
a) todas las nacionalidades estén representadas;
b) todas las nacionalidades estén representadas excepto los italianos.
5.46 Una urna contiene 3 bolas verdes, 2 azules y 4 rojas. En una muestra aleatoria de 5 bolas, encuentre la probabilidad de que se seleccionen bolas azules y al menos una roja.
5.47 Estudios de población de biología y el ambiente a menudo etiquetan y sueltan a sujetos con la finalidad de estimar el tamaño y el grado de ciertas características en la población. Se capturan 10 animales de una población que se piensa extinta (o cerca de la extinción), se etiquetan y se liberan en cierta región.Después de un periodo se selecciona en la región una muestra aleatoria de 15 animales del tipo. ¿Cuál es la probabilidad de que 5 de estos seleccionados sean animales etiquetados si hay 25 animales de este tipo en la región?
5.48 Una compañía grande tiene un sistema de inspección para los lotes de compresores pequeños que se compran a los vendedores. Un lote típico contiene 15 compresores. En el sistema de inspección se selecciona una muestra aleatoria de 5 y todos se prueban. Suponga que en el lote de 15 hay 2 compresores defectuosos.
a) ¿Cuál es la probabilidad de que para una muestra dada haya 1 compresor defectuoso?
b) ¿Cuál es la probabilidad de que la inspección descubra ambos compresores defectuosos?
5.49 Una fuerza de tarea gubernamental sospecha que algunas fábricas infringen los reglamentos federales contra la contaminación ambiental en cuanto a la descarga de cierto tipo de producto. Veinte empresas están bajo sospecha pero no todas se pueden inspeccionar. Suponga que 3 de las empresas infringen los reglamentos.
a) ¿Cuál es la probabilidad de que la inspección de 5 empresas no encuentre ninguna infracción?
b) ¿Cuál es la probabilidad de que el plan anterior encuentre a dos que infringen el reglamento?
5.50 Cada hora, una máquina llena 10,000 latas de bebida gaseosa, entre las cuales se producen 300 con un llenado insuficiente. Cada hora se elige al azar una muestra de 30 latas y se verifica el número de onzas de gaseosa. Denote con X el número de latas seleccionadas que tiene llenado insuficiente. Encuentre la probabilidad de que habrá al menos una con llenado insuficiente entre las muestras dadas.



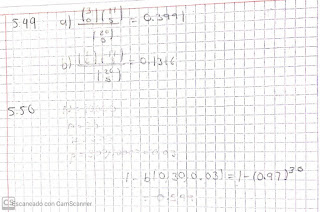


Comentarios
Publicar un comentario